

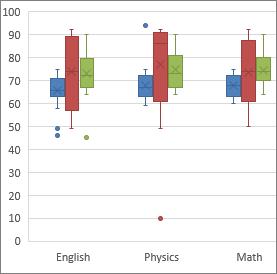
However the box plots in these examples show very different distributions of views. The medians (which generally will be close to the average) are all at the same level. Same median, different distribution – See examples (1), (2), and (3).The Items in Detail reports can be used to explore this further. The long upper whisker in the example means that students views are varied amongst the most positive quartile group, and very similar for the least positive quartile group. This shows that many students have similar views at certain parts of the scale, but in other parts of the scale students are more variable in their views. The 4 sections of the box plot are uneven in size – See example (1).This also suggests an area of difference that could be explored further in the Items in Detail reports and through consultation. Your school box plot is much higher or lower than the national reference group box plot. Any obvious difference between box plots for comparative groups is worthy of further investigation in the Items at a Glance reports. Obvious differences between box plots – see examples (1) and (2), (1) and (3), or (2) and (4).Follow this up by looking at the Items at a Glance reports. For example, the box plot for boys may be lower or higher than the equivalent plot for girls. One box plot is much higher or lower than another – compare (3) and (4) – This could suggest a difference between groups.This suggests students hold quite different opinions about this aspect or sub-aspect. The box plot is comparatively tall – see examples (1) and (3).
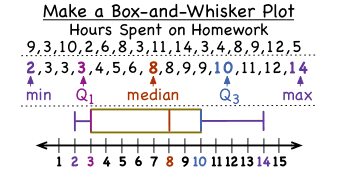
This suggests that overall students have a high level of agreement with each other. The box plot is comparatively short – see example (2).Some general observations about box plots The diagram below shows a variety of different box plot shapes and positions. They provide a useful way to visualise the range and other characteristics of responses for a large group. Interpreting box plots/Box plots in generalīox plots are used to show overall patterns of response for a group. Whiskers often (but not always) stretch over a wider range of scores than the middle quartile groups. The upper and lower whiskers represent scores outside the middle 50%. Twenty-five percent of scores fall below the lower quartile. Seventy-five percent of the scores fall below the upper quartile. The middle 50% of scores fall within the inter-quartile range. The range of scores from lower to upper quartile is referred to as the inter-quartile range. The middle “box” represents the middle 50% of scores for the group.

Half the scores are greater than or equal to this value and half are less. The median (middle quartile) marks the mid-point of the data and is shown by the line that divides the box into two parts. Usually we label these groups 1 to 4 starting at the bottom. The lines dividing the groups are called quartiles, and the groups are referred to as quartile groups. That is, 25% of all scores are placed in each group. Then four equal sized groups are made from the ordered scores. They enable us to study the distributional characteristics of a group of scores as well as the level of the scores.
How to do box and whisker plot how to#
How to read a box plot/Introduction to box plotsīox plots are drawn for groups of scale scores.


 0 kommentar(er)
0 kommentar(er)
